Cosmology Tutorial

Previous Section

Part 1: Observations of Global Properties
Part 2: Homogeneity and Isotropy; Many Distances; Scale Factor
Part 3: Spatial Curvature; Flatness-Oldness; Horizon
Part 4: Inflation; Anisotropy and Inhomogeneity

Spatial Curvature

One consequence of general relativity is that the curvature of space depends on the ratio of rho to rho(crit) . We call this ratio Omega rho/rho(crit). For Omega less than 1, the Universe has negatively curved or hyperbolic geometry. For Omega 1, the Universe has Euclidean or flat geometry. For Omega greater than 1, the Universe has positively curved or spherical geometry. We have already seen that the zero density case has hyperbolic geometry, since the cosmic time slices in the special relativistic coordinates were hyperboloids in this model.

The figure above shows the three curvature cases plotted along side of the corresponding a(t)'s. These a(t) curves assume that the cosmological constant is zero, which is not the current standard model. Omega > 1 still corresponds to a spherical shape, but could expand forever even though the density is greater than the critical density because of the repulsive gravitational effect of the cosmological constant.

The age of the Universe depends on Omega_o as well as H_o. For Omega=1, the critical density case, the scale factor is

a(t)
(t/t_o)^2/3

and the age of the Universe is

t_o
(2/3)/H_o

while in the zero density case, Omega=0, and

a(t)
t/t_o         with       t_o 1/H_o

If Omega_o is greater than 1 the age of the Universe is even smaller than (2/3)/H_o.

The figure above shows the scale factor vs time measured from the present for H_o 65 km/sec/Mpc and for Omega_o 0 (green), Omega_o 1 (black), and Omega_o 2(red). The age of the Universe is 15, 10 and 8.6 Gyr in these three models. The recollapse of the Omega_o 2 model occurs when the Universe is 11 times older than it is now, and all observations indicate Omega_o < 2, so we have at least 80 billion more years before any Big Crunch.

The value of H_o*t_o is a dimensionless number that should be 1 if the Universe is almost empty and 2/3 if the Universe has the critical density. In 1994 Freedman et al. (Nature, 371, 757) found H_o 80 +/- 17 and when combined with t_o 14.6 +/- 1.7 Gyr, we find that H_o*t_o 1.19 +/- 0.29. At face value this favored the empty Universe case, but a 2 standard deviation error in the downward direction would take us to the critical density case. Since both the age of globular clusters used above and the value of H_o depend on the distance scale in the same way, an underlying error in the distance scale could make a large change in H_o*t_o. In fact, recent data from the HIPPARCOS satellite suggest that the Cepheid distance scale must be increased by 10%, and also that the age of globular clusters must be reduced by 20%. If we take the latest HST value for H_o 72 +/- 8 (Freedman et al. 2001, ApJ, 553, 47) and the latest globular cluster ages giving t_o 13.5 +/- 0.7 Gyr, we find that H_o*t_o 0.99 +/- 0.12 which is consistent with an empty Universe, but also consistent with the accelerating Universe that is the current standard model.

Flatness-Oldness Problem

However, if Omega_o is sufficiently greater than 1, the Universe will eventually stop expanding, and then Omega will become infinite. If Omega_o is less than 1, the Universe will expand forever and the density goes down faster than the critical density so Omega gets smaller and smaller. Thus Omega 1 is an unstable stationary point unless the expansion of the universe is accelerating, and it is quite remarkable that Omega is anywhere close to 1 now.

The figure above shows a(t) for three models with three different densities at a time 1 nanosecond after the Big Bang. The black curve shows the critical density case with density 447,225,917,218,507,401,284,016 gm/cc. Adding only 1 gm/cc to this 447 sextillion gm/cc causes the Big Crunch to be right now! Taking away 1 gm/cc gives a model with Omega that is too low for our observations. Thus the density 1 ns after the Big Bang was set to an accuracy of better than 1 part in 447 sextillion. Even earlier it was set to an accuracy better than 1 part in 10⁵⁹! Since if the density is slightly high, the Universe will die in an early Big Crunch, this is called the "oldness" problem in cosmology. And since the critical density Universe has flat spatial geometry, it is also called the "flatness" problem -- or the "flatness-oldness" problem. Whatever the mechanism for setting the density to equal the critical density, it works extremely well, and it would be a remarkable coincidence if Omega_o were close to 1 but not exactly 1.

Manipulating Space-Time Diagrams

The critical density model is shown in the space-time diagram below.

Note that the worldlines for galaxies are now curved due to the force of gravity causing the expansion to decelerate. In fact, each worldline is a constant factor times a(t) which is (t/t_o)^2/3 for this Omega_o 1 model. The red pearshaped object is our past lightcone. While this diagram is drawn from our point-of-view, the Universe is homogeneous so the diagram drawn from the point-of-view of any of the galaxies on the diagram would be identical.

The diagram above shows the space-time diagram drawn on a deck of cards, and the diagram below shows the deck pushed over to put it into A's point-of-view.

Note that this is not a Lorentz transformation, and that these coordinates are not the special relativistic coordinates for which a Lorentz transformation applies. The Galilean transformation which could be done by skewing cards in this way required that the edge of the deck remain straight, and in any case the Lorentz transformation can not be done on cards in this way because there is no absolute time. But in cosmological models we do have cosmic time, which is the proper time since the Big Bang measured by comoving observers, and it can be used to set up a deck of cards. The presence of gravity in this model leads to a curved spacetime that can not be plotted on a flat space-time diagram without distortion. If every coordinate system is a distorted representation of the Universe, we may as well use a convenient coordinate system and just keep track of the distortion by following the lightcones.

Sometimes it is convenient to "divide out" the expansion of the Universe, and the space-time diagram shows the result of dividing the spatial coordinate by a(t). Now the worldlines of galaxies are all vertical lines.

This division has expanded our past line cone so much that we have to replot to show it all:

If we now "stretch" the time axis near the Big Bang we get the following space-time diagram which has straight line past lightcones:

This kind of space-time diagram is called a "conformal" space-time diagram, and while it is highly distorted it makes it easy to see where the light goes. This transformation we have done is analogous to the transformation from the side view of the Earth on the left below and the Mercator chart on the right.

Note that a constant SouthEast course is a straight line on the Mercator chart which is analogous to having straight line past lightcones on the conformal space-time diagram.

Also remember that the Omega_o 1 spacetime is infinite in extent so the conformal space-time diagram can go on far beyond our past lightcone,

as shown above.

Other coordinates can be used as well. Plotting the spatial coordinate as angle on polar graph paper makes the translation to a different point-of-view easy. On the diagram below,

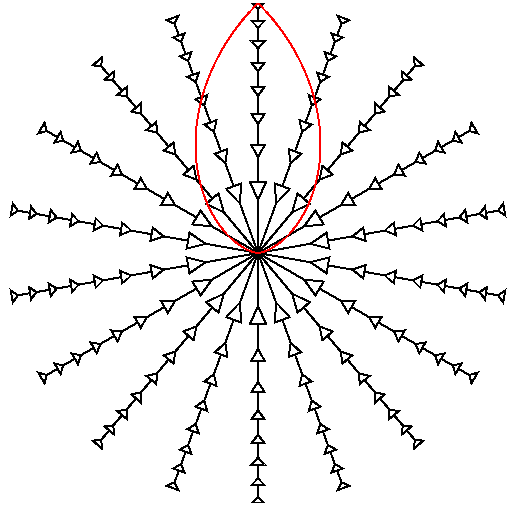
an Omega_o 2 model (which really is "round") is plotted this way with a(t) used as the radial coordinate. The past lightcone of an observer reachs halfway around the Universe in this model.

Horizon Problem

The conformal space-time diagram is a good tool use for describing the meaning of CMB anisotropy observations. The Universe was opaque before protons and electrons combined to form hydrogen atoms when the temperature fell to about 3,000 K at a redshift of 1+z 1090. After this time the photons of the CMB have traveled freely through the transparent Universe we see today. Thus the temperature of the CMB at a given spot on the sky had to be determined by the time the hydrogen atoms formed, usually called "recombination" even though it was the first time so "combination" would be a better name. Since the wavelengths in the CMB scale the same way that intergalaxy distances do during the expansion of the Universe, we know that a(t) had to be 0.0009 at recombination. For the Omega_o 1 model this implies that t/t_o 0.00003 so for t_o about 14 Gyr the time is about 380,000 years after the Big Bang. This is such a small fraction of the current age that the "stretching" of the time axis when making a conformal space-time diagram is very useful to magnify this part of the history of the Universe.

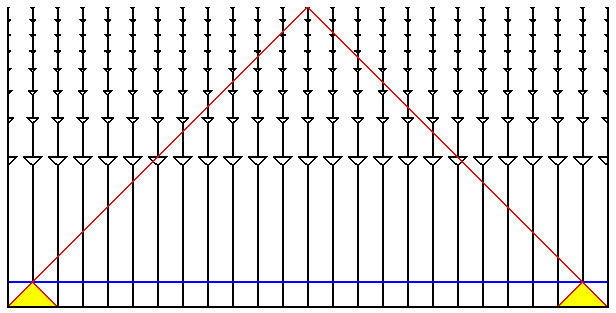
The conformal space-time diagram above has exaggerated this part even further by taking the redshift of recombination to be 1+z 144, which occurs at the blue horizontal line. The yellow regions are the past lightcones of the events which are on our past lightcone at recombination. Any event that influences the temperature of the CMB that we see on the left side of the sky must be within the left-hand yellow region. Any event that affects the temperature of the CMB on the right side of the sky must be within the right-hand yellow region. These regions have no events in common, but the two temperatures are equal to better than 1 part in 10,000. How is this possible? This is known as the "horizon" problem in cosmology.

Next Section

Ned Wright's home page

1996-2003 Edward L. Wright. Last modified 30 Aug 2003